Anatomy of a Wave
As we saw in the previous essay, sound is more than the physical forces in which it manifests. But just as much, these forces don't become sound until something about them repeats.
We generally represent that something as a value: amplitude. For example, for a sound in air, the amplitude is the measure of the pressure at some point in the room. For a string, the amplitude might be the distance the string is displaced measured perpendicular to the body of the instrument. Amplitude is customarily designated by a capital \(A\). There's more than one way to measure amplitude, and understanding this will matter in certain situations, such as understanding the proper technique for setting up microphones, or configuring the pickups in an electric guitar. Our understanding of the characteristics of sound—how repetition works—will apply to any measurement. But it is worth remembering that amplitude is produced with the act of measurement—even if this is done biologically by our ears. In the case of electronic sounds, this measurement is the voltage of some specific circuit element. Often “measuring” some other element of the circuit by rewiring the output (one of the techniques of circuit bending), will give drastically different results. In the circuit, as in the world, there is no correct way to measure amplitude, only conventional and unconventional ways.
When we measure this amplitude as it changes over time, we say that amplitude is a function of time. Another way of saying this same thing is that we are measuring amplitude in the time domain. Time is generally represented by a lower case \(t\). Instead, we could also measure some kind of aggregate amplitude, like the average (RMS) amplitude over a period of time, or over the whole song. As we will see later, we can also measure the aggregate amplitude at particular frequencies over a certain duration, in which case we would talk about amplitude as a function of frequency, or amplitude in the frequency domain. In general, a function is just an association between two different things. It's one thing measured according to another, like gas mileage measured according to the slope of a hill. The domain is the term of this relationship that we start with, so at a time we already know about (the domain), we measure an amplitude.
Amplitude, then, is generally measured as a relationship, and it can be measured according to different relationships. Repetition can only exist in these relationships, and this raises similar philosophical questions as for sound itself. That is: are we measuring time and measuring amplitude and creating a relationship between these measurements? Or does the relationship between time and amplitude exist in the world, waiting for us to measure it? Unlike the different ways to physically measure amplitude, we can to a certain extent abstractly translate between different relationships after we have measured them. That is, given an amplitude measured in the frequency domain, we can convert it to the time domain, and vice versa. There are, however, some very important caveats to these transformations that we will explore later.
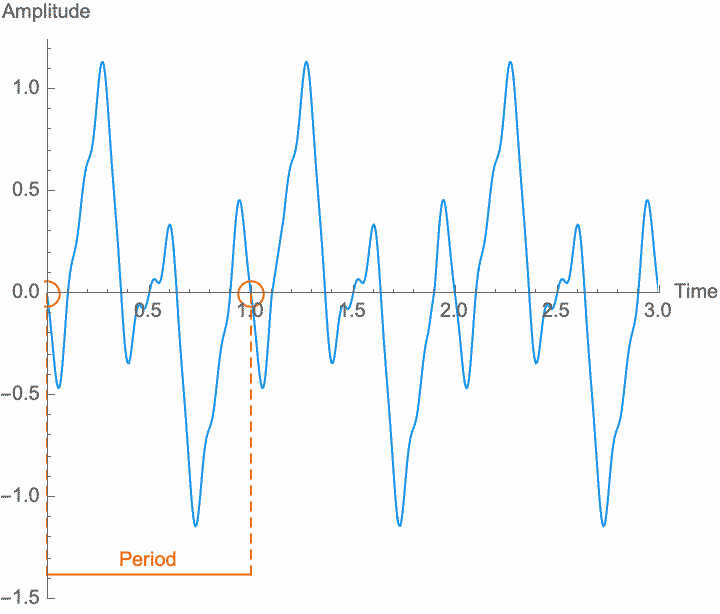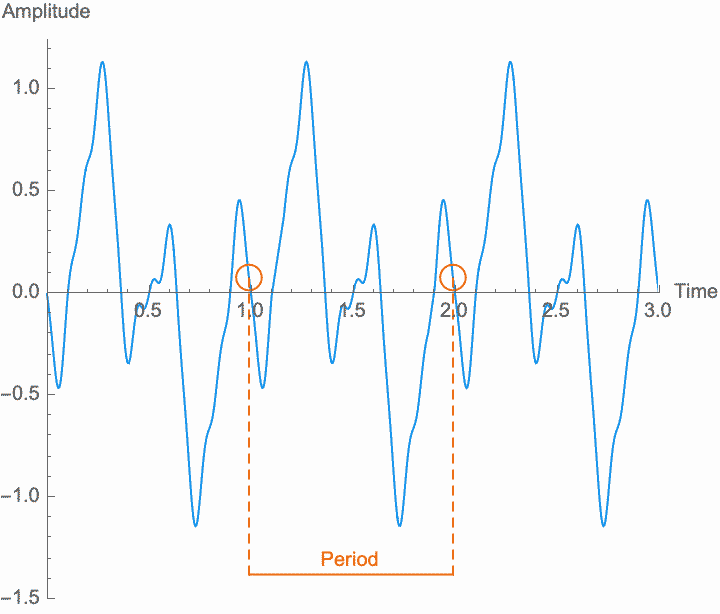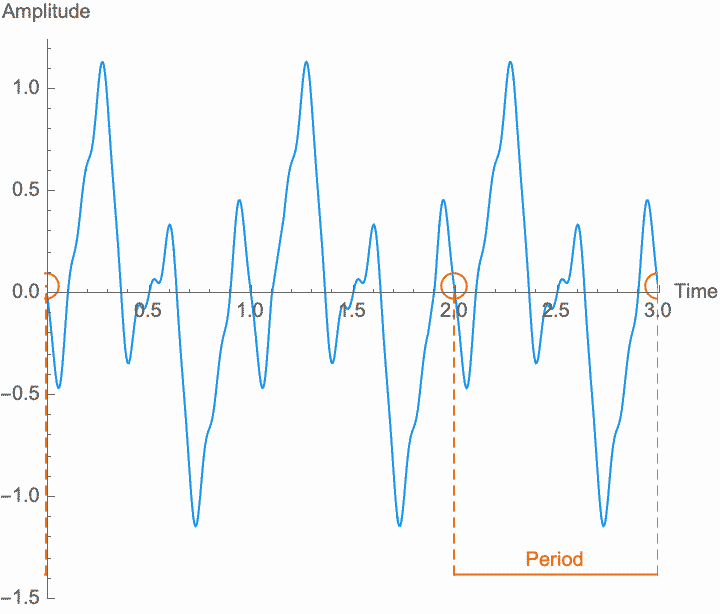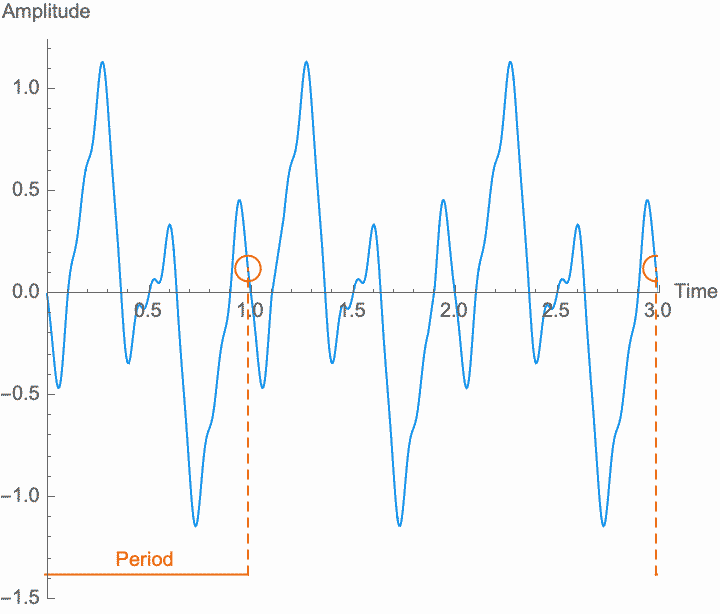
A sound is just repetition. While we will see later that we can understand non-repetitive things according to how they relate to repetitive phenomena, for now it is useful to talk about sound as absolutely and purely repetitive. We call this absolute repetition periodic. Anything that repeats absolutely, anything that is periodic, will always have the same amplitude for any two points in time that are separated by a certain duration, known as the period. Period is customarily designated by a capital letter \(T\). The period is the length of time during which an entire pattern of amplitudes repeats. In so far as a sound is repetitive, the period is the same for every single point in time. In practice, sounds begin, end, and change over time, and so nothing is perfectly repetitive. Nevertheless, it is only through the abstract concept of perfect repetition that we can understand the imperfect repetition of actual sounds. This concept of perfect repetition is the measuring rod, so to speak, which we can hold up to a sequence of events in order to talk about its repetitiveness.
It's often more useful to talk about the reciprocal of the period, the frequency of the wave. Frequency is customarily designated by the lowercase letter \(f\). While the period measures how long a repetition takes, frequency measures how often it happens. These are just different ways of thinking about the same thing, since how long something takes will determine how often it can happen, or how often it happens will determine how long it can take. We can express this mathematically with the equation \(f = 1/T\).
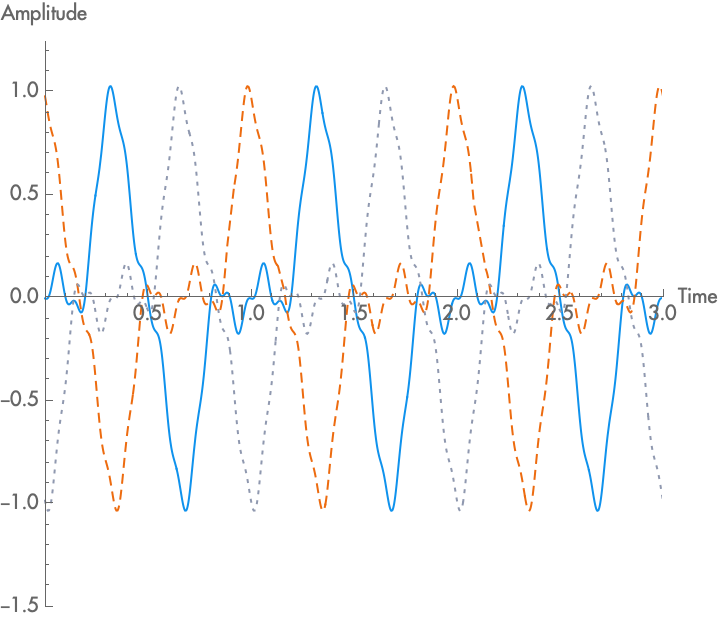
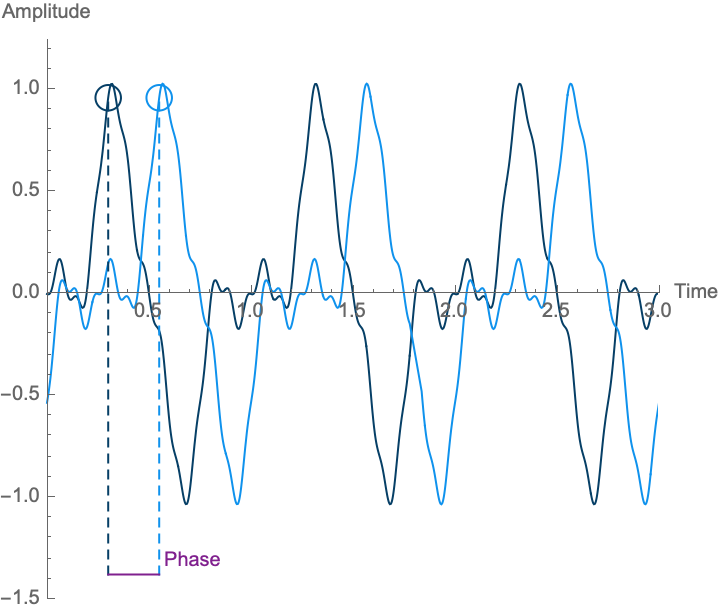
Each period of a periodic wave can be laid out in time differently, such that at any point in time, different parts of that wave could be happening. We call these different ways a wave can be placed in time the different \(phases\) of the wave. Note, however, that with a perfectly periodic wave, any point on the wave is a repetition of another point from one period earlier, all the way back to the beginning of time, and all the way forward to infinity. As such, there is no real beginning to the wave, and so all of these different phases are in some sense equivalent. Phase only has consequences and can only be measured relative to a reference wave, although the reference wave might only be conceptual. Given a reference wave, the amount of time by which the wave is delayed or advanced relative to the reference wave is called the phase. Phase is customarily designated by the lowercase Greek letter phi: \(\phi\). Because phase is relative, it is always a relationship between two waves, and one can always select or produce a third wave that will have a different phase relationship.
The Independence of Amplitude, Frequency, and Phase
Any sound whatsoever can be described according to these three independent characteristics: amplitude, frequency, and phase. What we mean by independent is that, under certain circumstances, altering one value will have no effect on the other values. But only under certain circumstances.
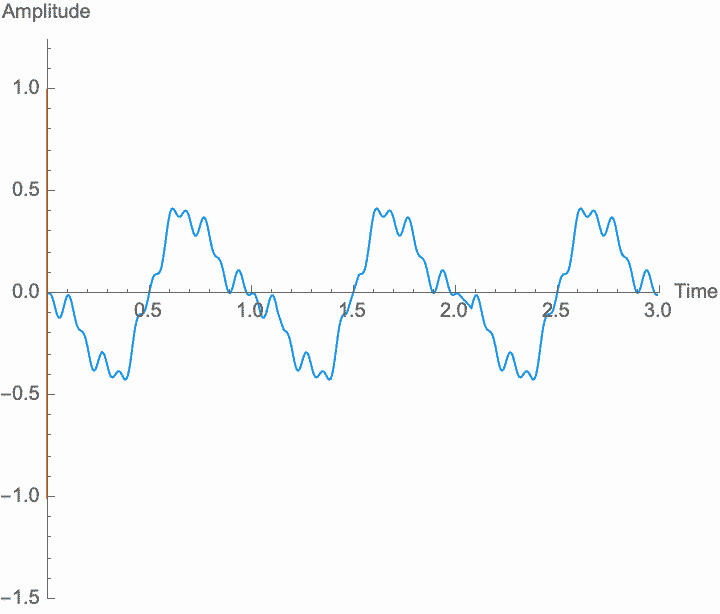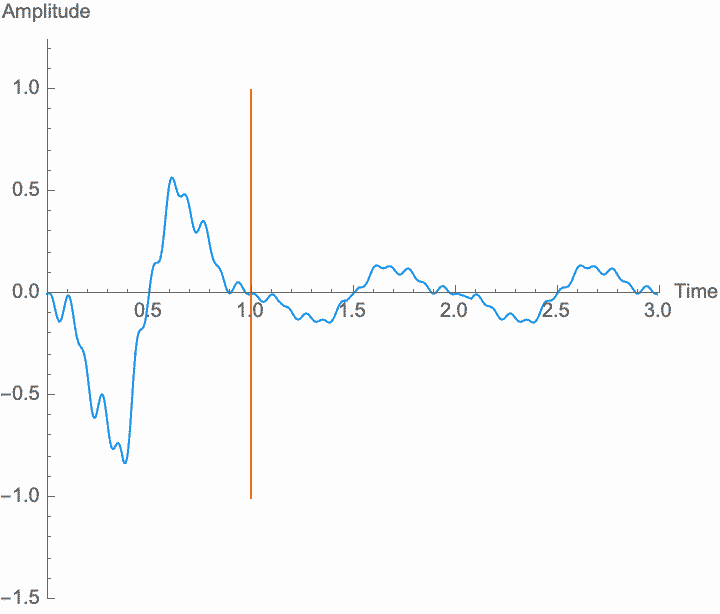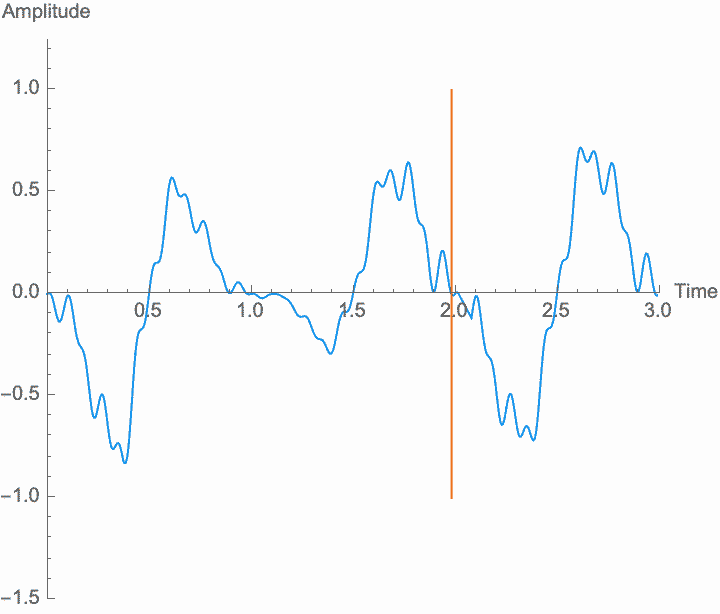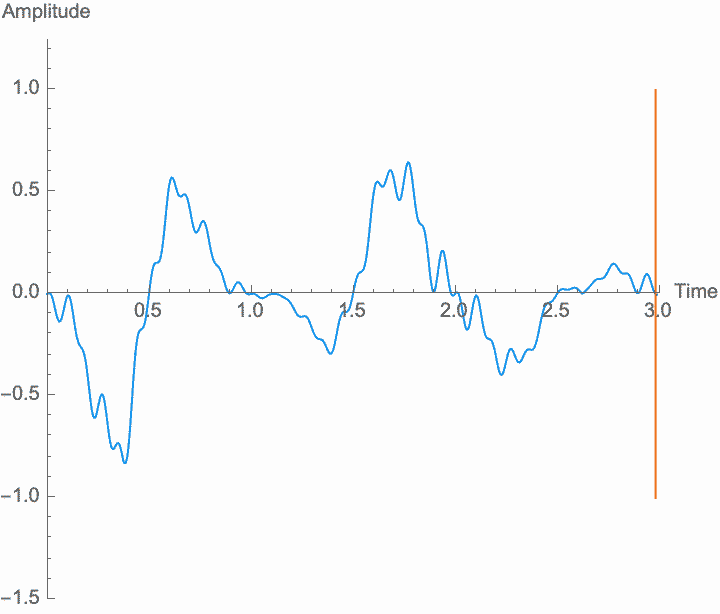
Amplitude is the material of which sound is made. If there is no amplitude, there is no sound, and just how much amplitude we have (on average) determines how much sound there is—the power, or volume, or loudness of the sound. But what makes the sound a sound, repetition, is determined by the shape of the amplitude in relation to time, not its size. Any transformations of amplitude which preserve its shape won't affect these characteristics. Specifically, if we scale the amplitude of the wave—if we amplify it, which is the same thing as multiplying the amplitude by a constant factor—the shape of the sound won't be affected. Amplification just gives us more or less sound. Note, however, that if the amplification factor itself changes at a frequency similar to the wave frequency, the shape of the wave is affected, and the frequency and general character of the sound will change. This is known as amplitude modulation or AM.
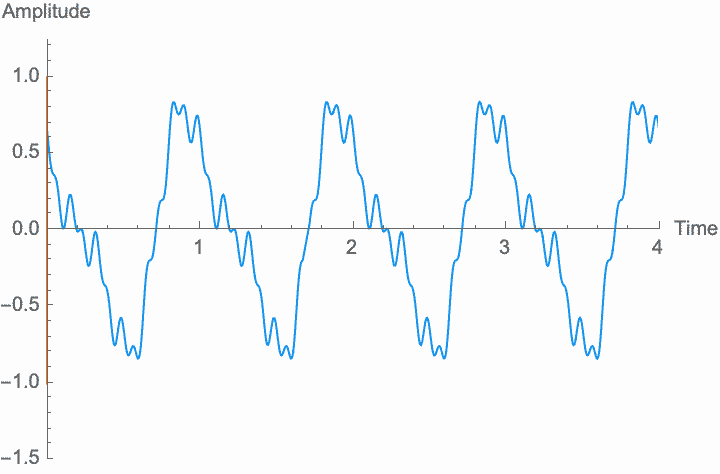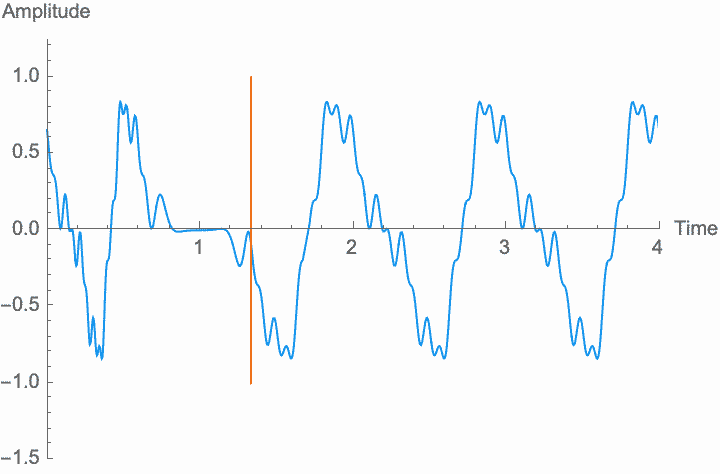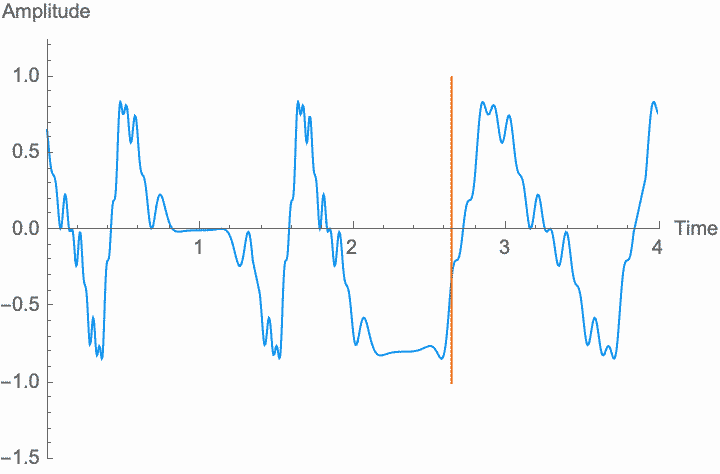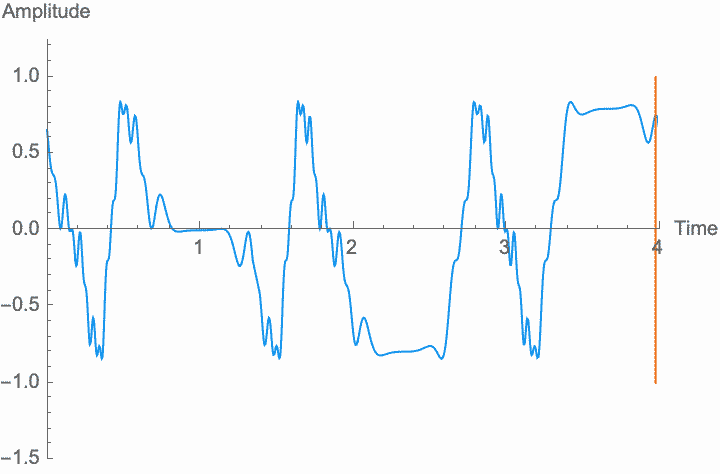
Frequency, or period, is the simplest possible measurement of repetition. Perceptually, the frequency of a wave determines its pitch, while the shape of the wave within each period determines the character of the sound. Changing the frequency—scaling the temporal dimension of the wave—will change the pitch without changing the overall amplitude and without changing the shape, or character, of the sound. However, as with amplitude modulation, if the rate at which we change the frequency is high enough, the shape of the wave and the character of the sound do change. This is known as frequency modulation or FM. However, the method of digital synthesis known by this term generally uses phase modulation (see below), rather than frequency modulation.
Phase is the relationship between a wave and some reference. Phase determines how multiple waves combine. In addition, phase relationships are perceptually used to infer the distance and direction of sounds in a space—since a greater distance means a greater delay, and a more indirect sound means more phase smearing between different frequencies. Since phase is a relationship, differing constant phases have no effect on frequency or amplitude, which are not relational parameters.
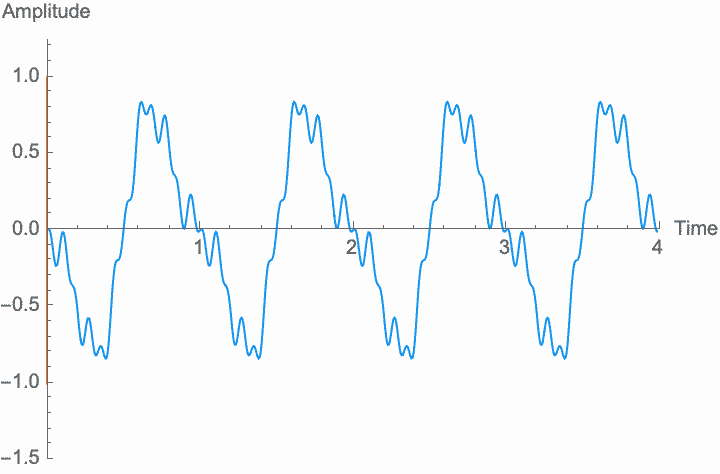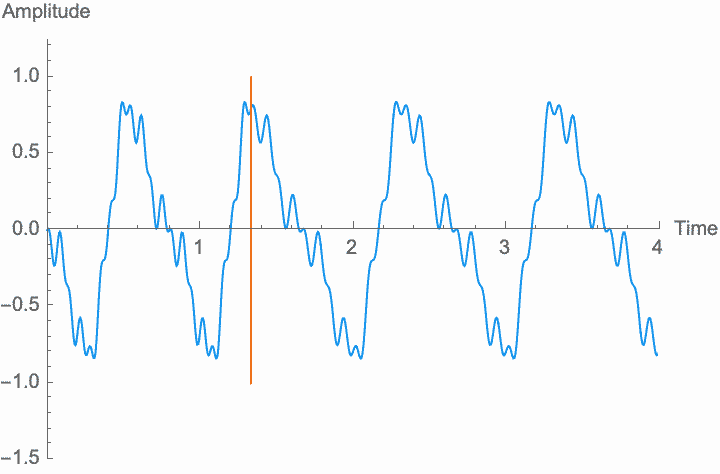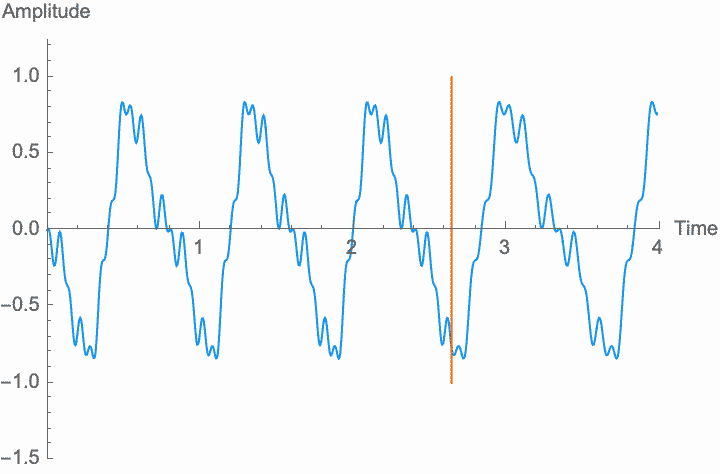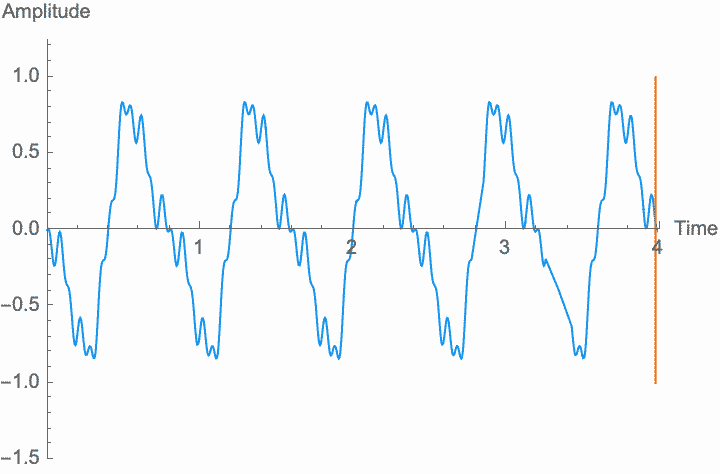
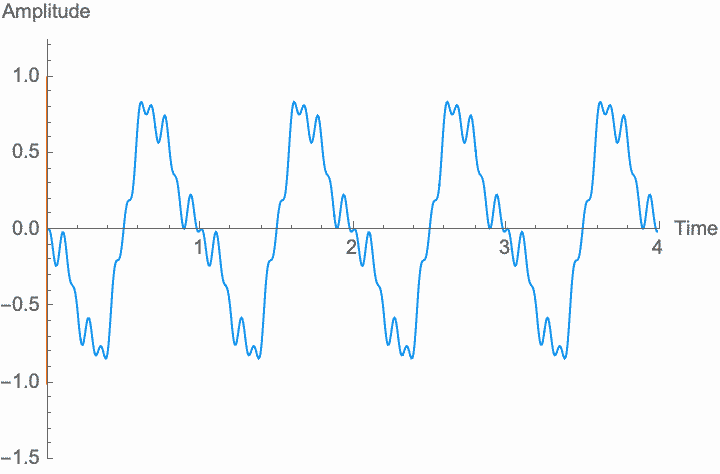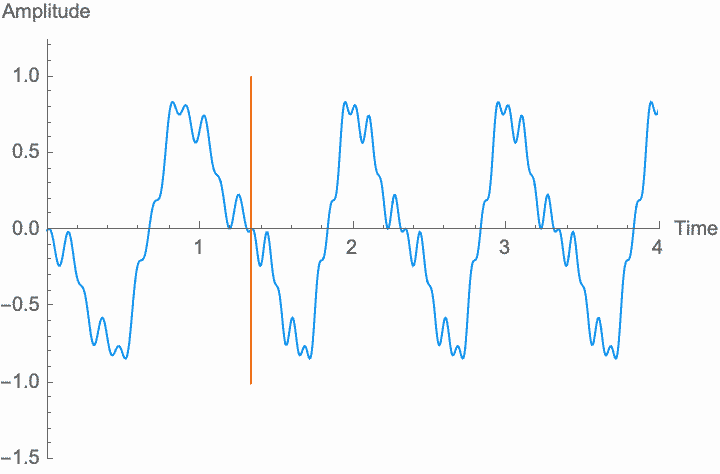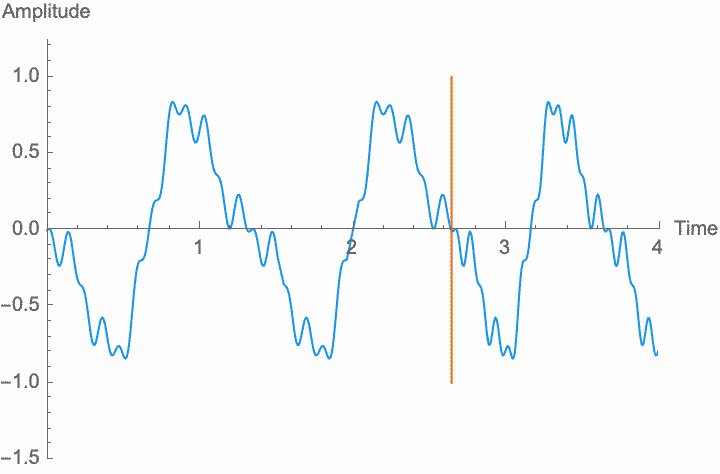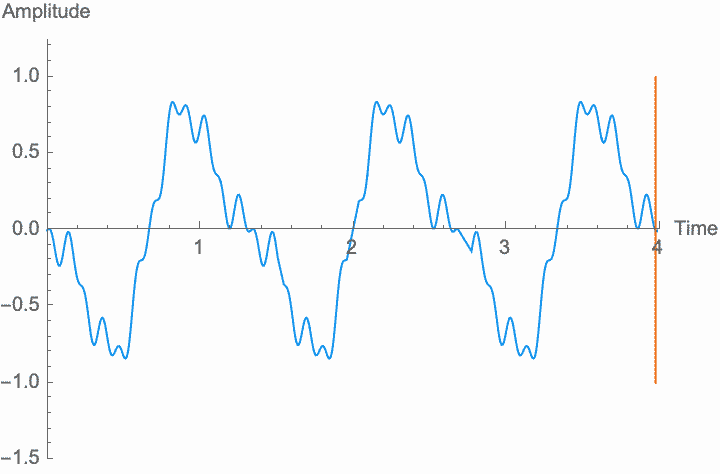
However, a changing phase always has an affect on the frequency. In fact, there is no way to distinguish between changing the phase of a wave at a constant rate and altering its frequency. Looking at the figures on the left, you can see that continually shifting the phase of the wave in one direction effectively scrunches together the wave, shortening its period and raising its frequency. Continually shifting the phase in the other direction stretches out the wave, lengthening its period and lowering its frequency. This is the basis of the Doppler effect, where quickly moving sound sources, such as a siren, are higher pitched when they are coming towards you (the phase is moving in one direction), and lower pitched when they are moving away (the phase is moving in the other direction). This is also the basis for chorus and flanger effects, where a slowly changing delay time (a changing phase) gives rise to a slowly changing frequency.
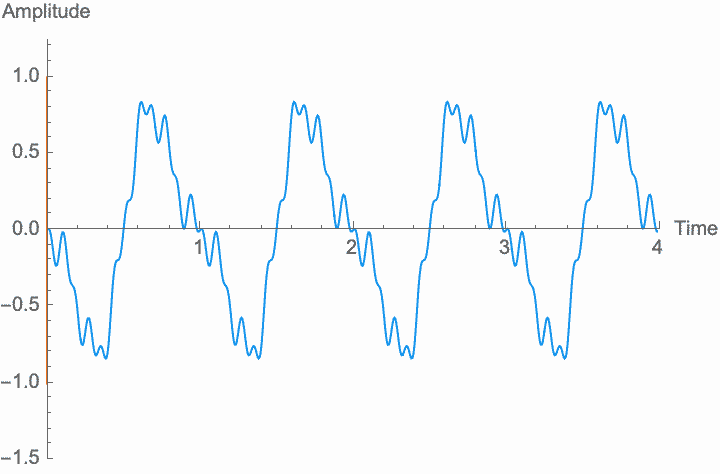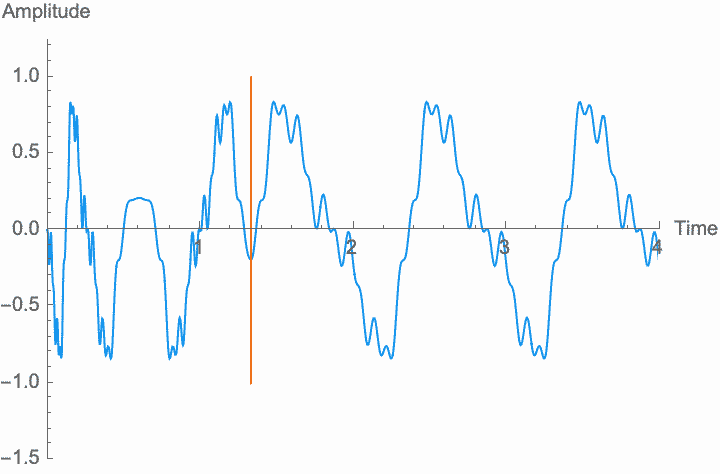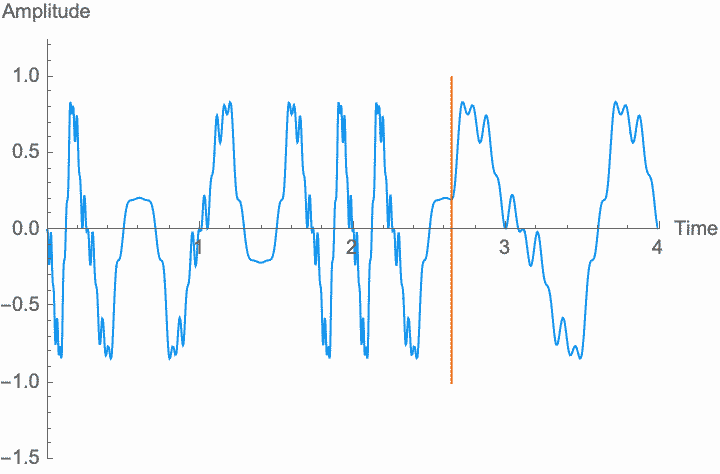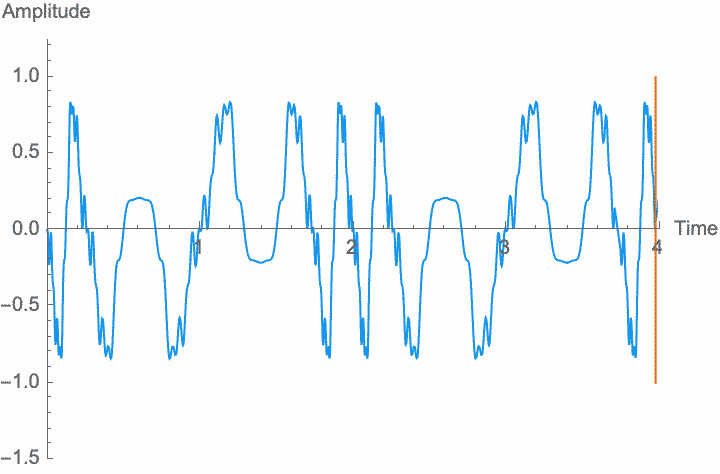
Just as with frequency and amplitude, if the rate at which phase changes is high enough, the shape of the wave and the character of the sound changes. This is known as phase modulation or PM.
In summary, while constant values of phase, frequency, and aggregate amplitude are completely independent of each other, when these values start to change they become increasingly entangled. As the rate of change increases, their entanglement becomes more obvious. When we are able to treat them independently, and when we will have to think about them as complex modulation, will depend on the context. But in general, if the rate of change of these parameters is sufficiently slow, then phase, frequency, and amplitude will be essentially independent.
On the one hand, phase, frequency, and amplitude are analytical terms. That is, these terms result from analyzing different parts of the single phenomenon of sound. As such, sound doesn't “have” an amplitude, or a frequency, or a phase. And as we dig further into these terms in this series, we will start to see limiting cases where it is difficult or impossible to define an exact frequency, amplitude, or phase. On the other hand, these analytical terms tell us real things about what sound is and how it functions. In the limiting case of an infinite and perfect wave, frequency, phase, and amplitude really are well defined and completely independent. Real world waves are neither infinite nor perfect, but it is only by constructing frequency, phase, and amplitude absolutely that we are able to see both the application and limits of these concepts. Concepts never quite meet the world. Our best concepts help us to clearly see the distance between concept and world, rather than obscuring that distance.
A Mathematical Representation of a Wave
We start with a mathematical representation of the function relating amplitude and time: \(\operatorname{wave}(t)\). \(\operatorname{wave}(t)\) is just a relationship between amplitude and time. Given some time \(t\) (or whatever value is inside the parentheses), \(\operatorname{wave}(t)\) is the amplitude of the wave at that time. Because \(\operatorname{wave}(t)\) is a sound, we know that it repeats, and so we know that there is some period \(T\) after which the amplitude of \(\operatorname{wave}(t)\) always returns to the same value. We can express this as:
If we amplify \(\operatorname{wave}(t)\) by some factor, that's just scaling (multiplying) the amplitude, that is, multiplying the function \(\operatorname{wave}(t)\) by some factor. For example, to amplify by 6dB (\(2 \times\)), we want \(2 \operatorname{wave}(t)\). We would write this as:
If, on the other hand, we want to change the frequency, that's the same as scaling (multiplying) \(t\) by some factor. So if, for example, we want to double the frequency, that's just saying we want things to happen twice as often, or that we want to get the value of \(\operatorname{wave}(t)\) as if time was passing twice as quickly. We would write this as:
Lastly, if we want to change the phase, that's the same as delaying or advancing time by some duration. So if, for example, we want to advance the phase by \(5\), that's just saying that we want the value of \(\operatorname{wave}(t)\) as if time was shifted forward by \(5\). We would write this as:
Putting it all together, we can represent phase shift, changing frequency, and amplification as:
It is possible to simplify all of this, however. If we shrink down \(\operatorname{wave}(t)\) such that its maximum amplitude is \(1\), then when we amplify this shrunk down \(\operatorname{wave}(t)\) by \(A\), the new maximum amplitude is \(1 \times A\), or just \(A\). That is, instead of an amplification factor, \(A\) is the amplitude itself. This is called normalization. We can also normalize the period, \(T\), by compressing or expanding \(\operatorname{wave}(t)\) in time, such that the period is exactly one. On the one hand, this means that multiplying by \(f\) gives us a frequency of \(1 \times f\), or just \(f\). On the other hand, this means that advancing the time by \(1\) advances it for exactly one period, and so we can represent phase as a fraction of one period. Unless otherwise specified, we can assume that when we express waves mathematically, they are normalized. Note, however, that sine and cosine waves, which we will discuss later, are conventionally normalized to have a period of \(2 \pi\), rather than \(1\).
Pulling all of this together, we can now read the following equation:
This equation describes a wave with amplitude \(A\), frequency \(f\), and phase \(\phi\). For a particular value of \(t\), this equation gives the amplitude of the wave at the instant \(t\). The period of this wave is the reciprocal of the frequency: \(T = 1/f\).
References
This essay will form the basis of many future essays in this series. However, if you don't want to wait, or if you just want to dig in deeper, the best place is probably a physics or acoustics textbook. Of course this will bring with it all the general problems with textbooks—lots of hand waving and very little about practical application.
For more information on phase and its relationship to the perception of proximity, see David Griesinger, “Phase Coherence as a Measure of Acoustic Quality” on akutek.info (2010). Griesinger is the engineer most responsible for the Lexicon 224 reverb.