

Phase, Delay, and Mixing
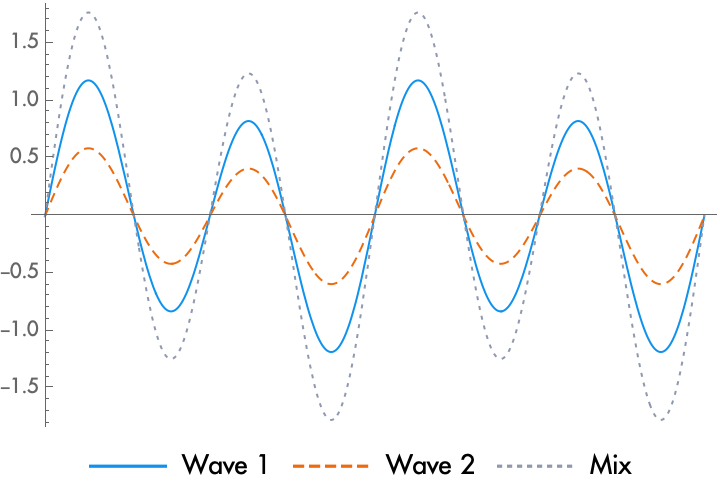
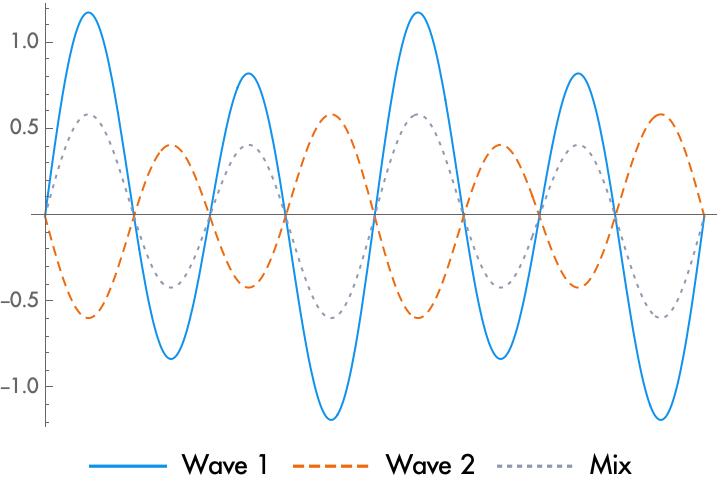
When we mix two waves together, we obtain a new waveform which is the addition of their amplitudes. While there are some boundary conditions where more complicated things happen, when physical waves encounter each other in a medium, such as air, usually the approximate effect is the same as mixing, or addition. When waves with different phases, frequencies, and shapes are joined together, sometimes the peaks are aligned, and the waves are rising or falling with each other. Other times, a part of one wave that is rising is aligned with a part of another wave that is falling. As you would suspect, when the peaks are aligned, the waves enhance each other and the amplitude grows. This is known as constructive interference. When the waves are negatively aligned, where one wave rises while another falls, the waves cancel out and the amplitude shrinks. This is known as destructive interference. Complex waves of different shapes will have some elements that are aligned, and some elements that are negatively aligned, and the resulting wave will change shape. This change of shape means that the spectrum of the wave changes.
In addition to alignment, each wave can have a different polarity. If you reverse the polarity of a wave, it rises where before it fell, and it falls where before it rose. When mixing a wave with reversed polarity, alignment becomes negative alignment, constructive interference becomes destructive interference, and vice versa. This can be a problem, for example, when two close microphones use different mechanisms and give two different polarities of the same signal.
When the waves that are mixed together have relatively unrelated spectra, you could look at the result as just one spectrum adding to another, just one sound and another sound, gathered together in the same spectrum. For example, two unrelated notes will produce a new wave shape, which means a new spectrum, but generally we just think about this as two different notes. This is why mixing works. This is also the power of spectra—we can decompose a complex waveform in which sounds have already been combined into its parts, into the individual sounds. But while mixing unrelated spectra involves a lot of technique, we will leave that for a different essay.
In sound design, we generally mix together related spectra, and end up with new kinds of sounds. This is a common technique in classical orchestration, where a melodic line might be shared by both a brass and woodwind instrument, for example, resulting in the overall impression of a new sound sharing some of the characteristics of each. Alternately, multiples of the same instrument can sound somewhat different from each individual instrument. For example, a single voice sounds different from a chorus, and the three strings for each note on the piano can blend together smoothly or roughly, giving more or less exactly tuned pianos very different sounds.
But really interesting things happen when you mix together very highly correlated spectra, such as a recorded instrument with a delayed copy of itself. To analyze this kind of mixing, we'll look at how the individual elements of the spectrum (sine waves) combine with each other.
Sine Waves of the Same Frequency
When a sine wave combines with another sine wave of the same frequency, the wave shape and frequency never change, but the phase and amplitude may change. This is one of the things that makes sine waves special. In general, when combined with another wave of the same shape, for every other kind of wave the resulting wave will be a different shape (although there could be a few specific phase differences that give the same shape). For sine waves, the result is always another sine wave of the same frequency, regardless of amplitude or phase difference.
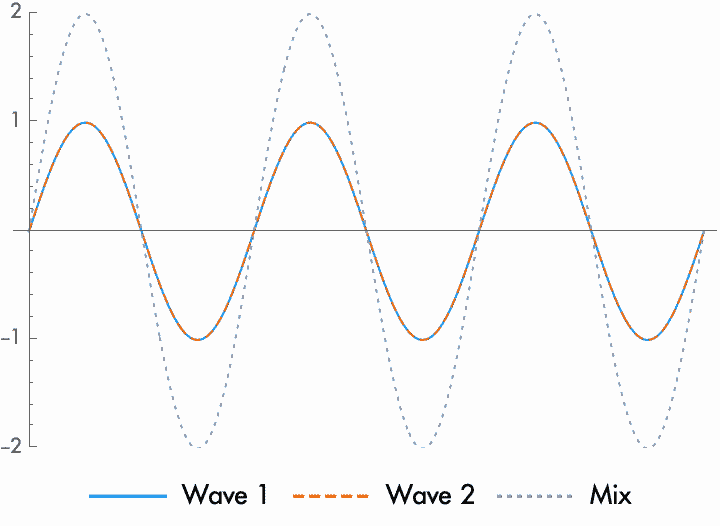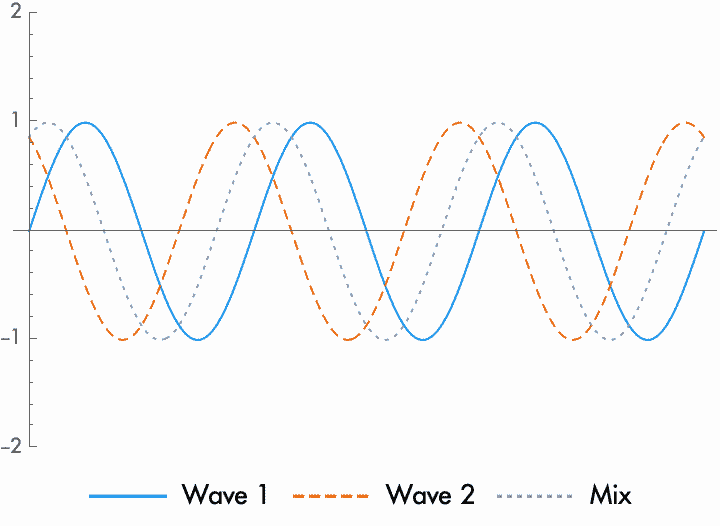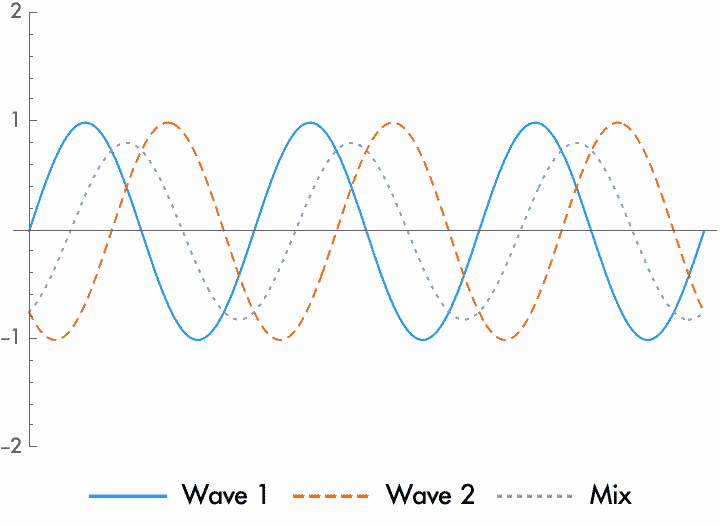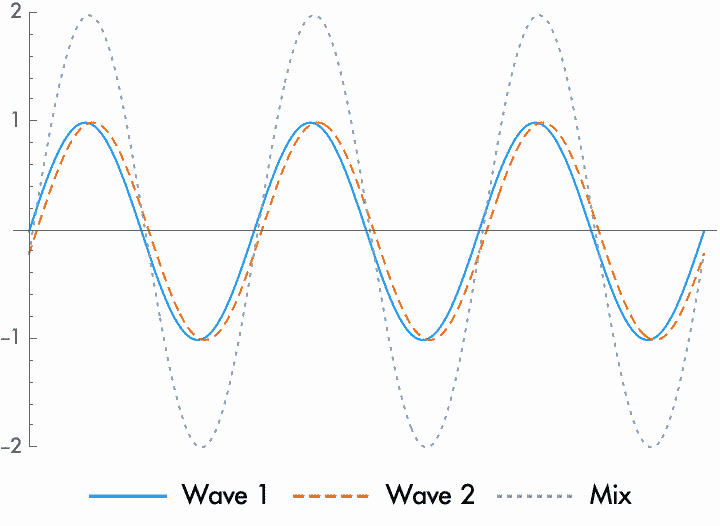
What this means is that when two sine waves combine, the result is completely dependent on the relative phase and amplitude of the two sine waves. When the sine waves are in phase, when the phase difference is small, then the amplitudes are added together. For waves of the same amplitude, the amplitude is doubled. When they are out of phase—when one sine wave is delayed by half a cycle, such that one rises when the other falls—then the amplitude shrinks, or is even altogether cancelled to silence for waves of the same amplitude. But in between these extremes, when the waves combine the result is an amplitude that grows only a little, shrinks only a little, or stays the same (while the phase shifts).
On average, when two unrelated sine waves of the same frequency are combined they will have a random phase alignment. Statistically, for sine waves of the same amplitude, this results in an average increase of \(4/\pi\) or \(1.27\). However, note that this is only going to be true on average, and only when the phases of the two waves are uncorrelated. For example, if you mix together four layered guitars, the resulting amplitude would be about \(1.27 \times 1.27 = 1.61\) times the amplitude of each individual guitar. But if you mix together four microphones recording the same guitar, these will have correlated phases and won't follow this statistical pattern.
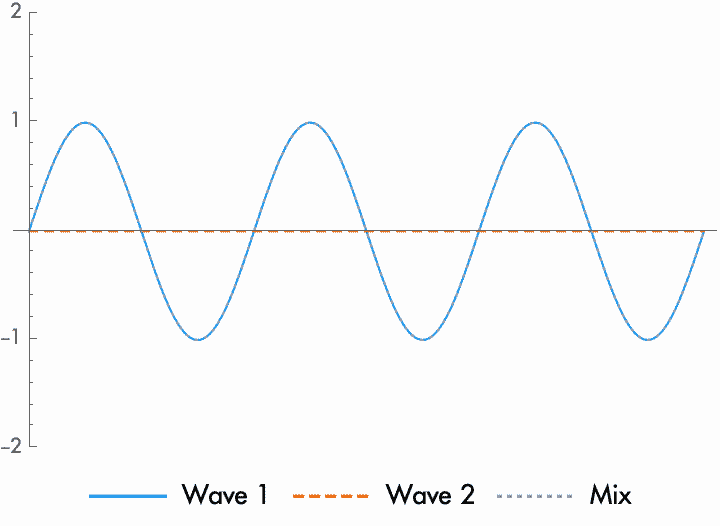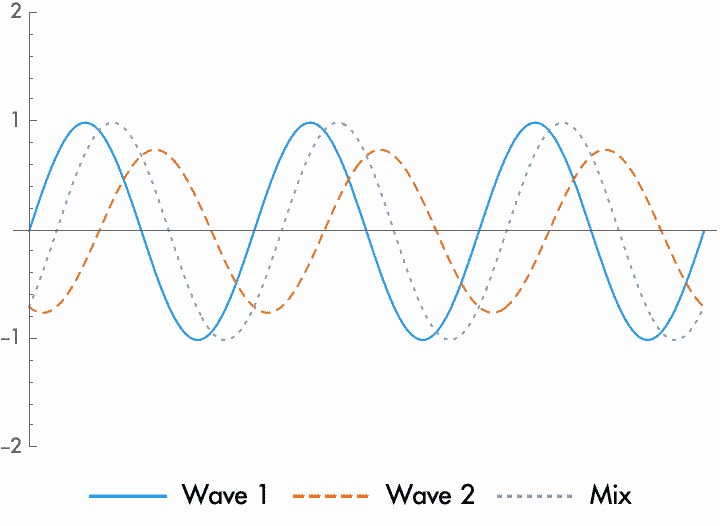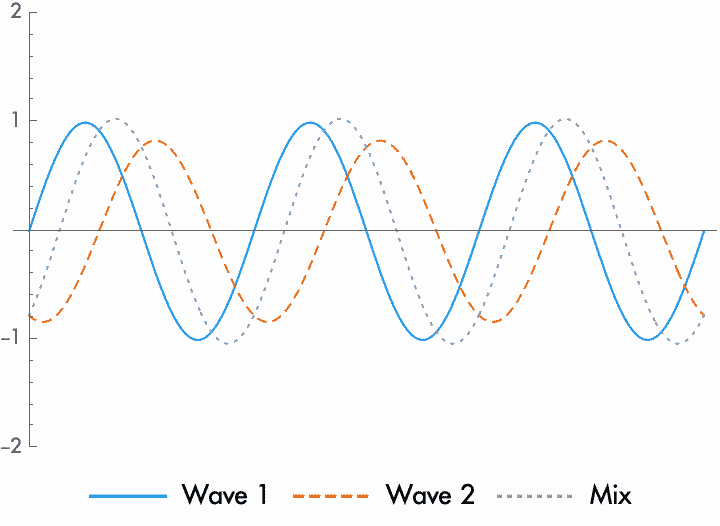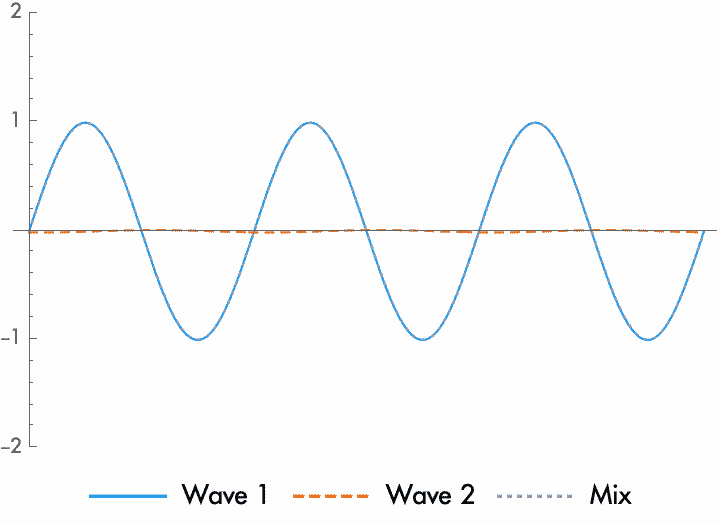
Adding together two sine waves will also change the phase of the resulting wave, unless the sine waves are exactly in phase or out of phase. How much the phase changes depends on the relative amplitude of the two waves. When the waves are close in amplitude, the new phase will be exactly in between the phase of the first and second wave. When one amplitude is larger than the other, the new phase will be closer to the wave with the higher amplitude.
Because a phase shift depends on the relative amplitude of the two waves, this means that by changing the amplitude of one or both waves, you can change the phase of the combined wave. Conversely, because the amplitude of the resulting wave depends on the relative phase of the waves, this means that by changing the relative phase, you can affect the amplitude. This relation between relative phase and amplitude is the basis for a huge number of audio effects, like phasers and filtering.
Because a sine wave is symmetrical, it has a fall corresponding to each rise, happening exactly one half cycle later. Changing the polarity of the wave, then, is the same as adding a phase difference of one half cycle. As we will see, this is not the case for all complex waves, although some complex waves are symmetrical. When mixing sine waves of different phases together, the phase difference of the resulting wave shifts between the phase of the first wave and the phase of the second, depending on the relative amplitudes of the two waves. When you continue to shift the amplitude past zero (changing the polarity of the wave), this change in polarity corresponds to a change in phase of half a cycle. As we further increase the amplitude, the mix of these waves moves towards this new phase, one half cycle beyond the first. Because of this, by changing the polarity and amplitude of any two sine waves, we can create a new wave with any phase. The exception is when the phase difference is zero or half a cycle, perfectly aligned or unaligned, in which case the new wave can only change amplitude and polarity, but not phase.
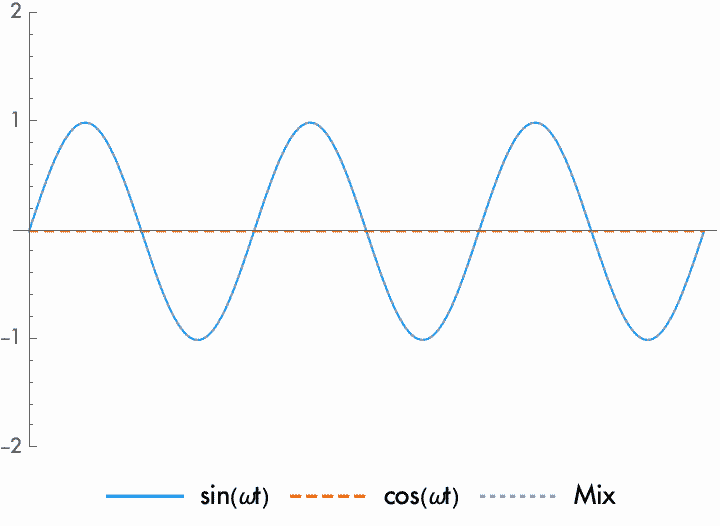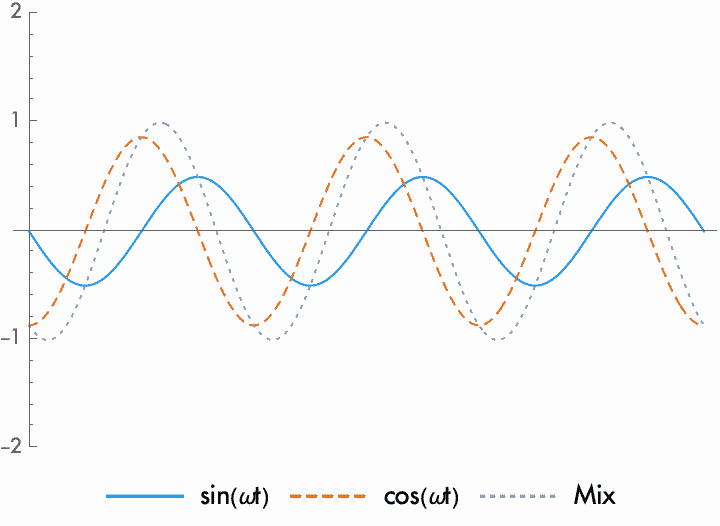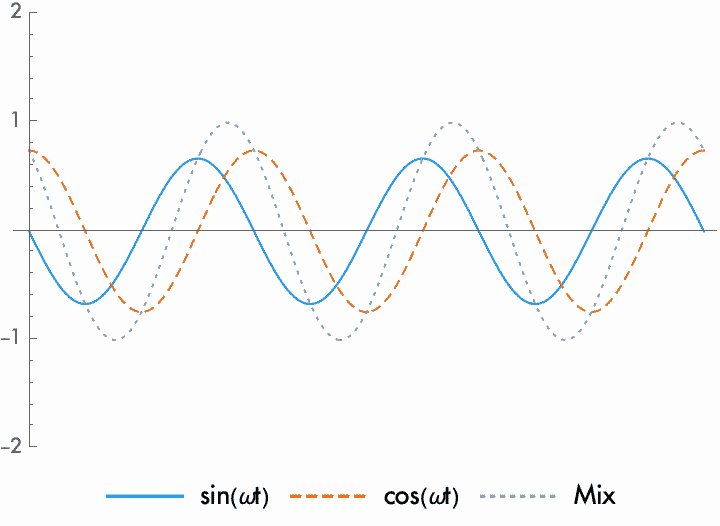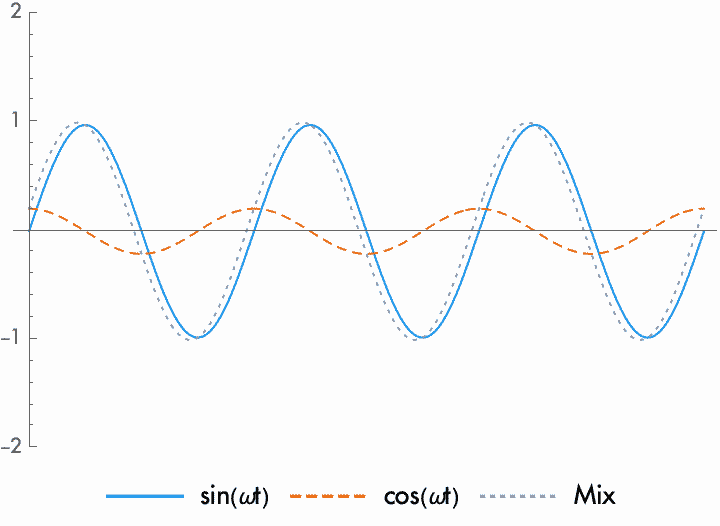
One particularly useful phase difference is the quarter cycle (90°, or \(\pi/2\) radians). Since reversing the polarity shifts the phase by half a cycle, reversing the polarity of a wave delayed by a quarter cycle exchanges the phase relationship. That is, if we start with two waves with one a quarter cycle advanced in phase from the other, if we reverse the polarity the phase shifts by one half cycle, and the wave is now a quarter cycle delayed. A sine wave that is delayed by a quarter cycle can be called a cosine wave, and the two waves are said to be in quadrature.
Sine Waves of Different Frequencies: Beat Frequencies
As we saw in the essay on the Anatomy of a Wave, changing the phase of a wave at a continuous rate is the exact same thing as altering its frequency. We can, then, think about the combination of two waves of different frequencies as the combination of two waves of the same frequency with a continually changing phase relationship. The phase of the higher frequency wave will be advancing at a constant rate relative to the lower, and the phase of the lower frequency wave will be advancing at a constant rate relative to the higher.
The phase difference between two sine waves determines the output amplitude. Since the phase difference between waves of different frequencies is constantly changing, the amplitude rises as the phases approach alignment, and then falls as the phases fall out of alignment, rising again as the waves approach alignment again. This fluctuation itself takes the form of a sine wave, where the rate is proportional to the difference between the two frequencies. There is, then, no difference between mixing together two sine waves and modulating the amplitude of one sine wave with another sine wave.
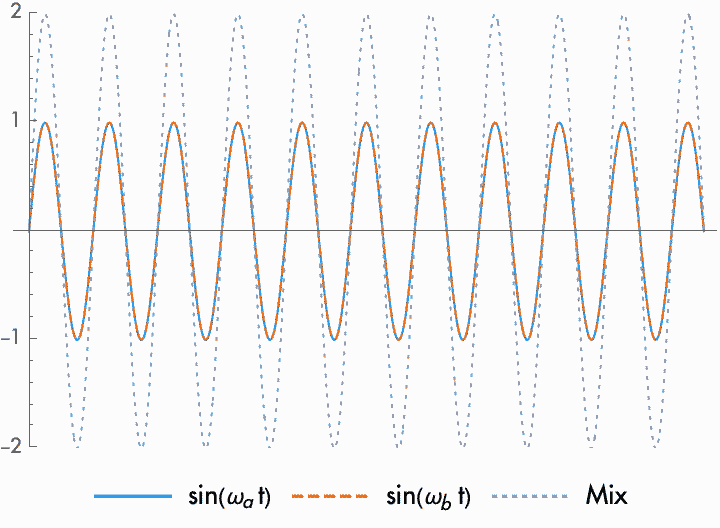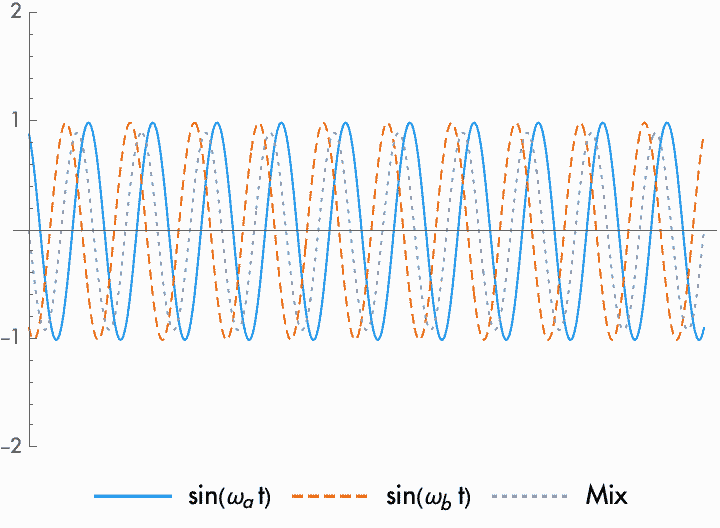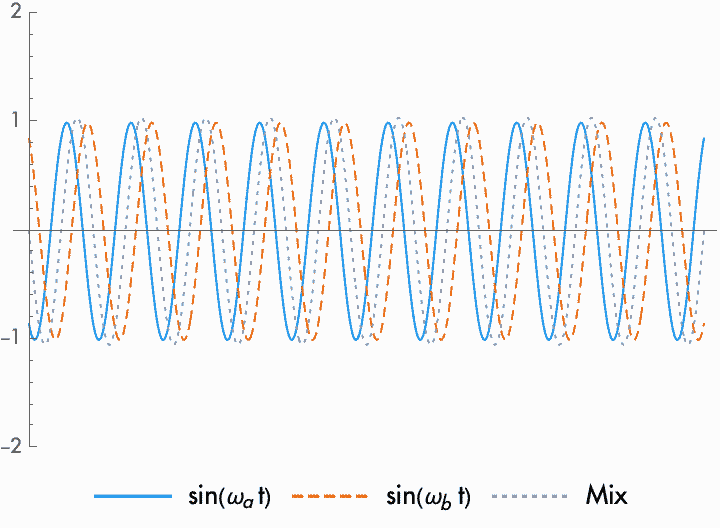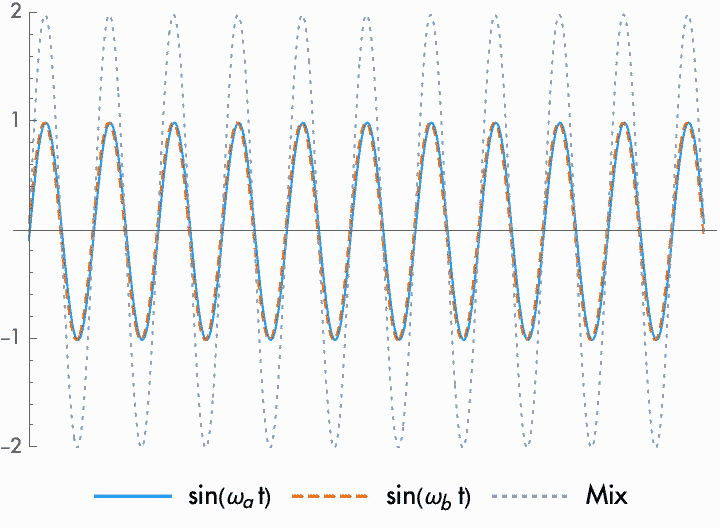
This frequency at which the amplitude fluctuates is known as the beat frequency. When the frequencies of the combined waves are close together, the difference in frequency and the resulting beat frequency will be slower. When the beat frequency is slow enough, we hear the combined waves as a single frequency with a fluctuating amplitude. When the combined waves are farther apart, the beat frequency enters into the audio range. However, while beat frequencies in the audio range can be important in certain circumstances, for the most part we don't perceive them. We just perceive two different sounds at two different frequencies.
So what's different about slower and faster beat frequencies? Are beat frequencies real frequencies or perceptual effects? When we combine waves of two different frequencies, will we get a single wave with a beat frequency, or just the two different frequencies?
To answer these questions, we have to return to the concept of a spectrum, and the concept of a wave. In the most formal sense, a spectrum identifies what a wave does from the beginning of time until the end of time, and every one of its frequency elements has a single, constant amplitude and phase. But we also think about a wave as something that unfolds over time, that might take on a particular spectrum during one particular time period, but another spectrum in another period. But for how long of a period? As we will discover, there's no way to consistently draw a line between the time over which a wave evolves and the time during which it repeats. Only repetition makes something a wave, but if the wave is also constantly evolving, how is it ever really repeating?
The answer always depends on your point of view. When we analyze the spectrum of a wave whose amplitude is slowly fluctuating over a big enough time scale, it will look like two different sine waves. Conversely, when we analyze the spectrum of sine waves of two frequencies over a short enough time scale, we will find only one sine wave with a varying amplitude. This is true not just in our own perception, but also for whatever tool we might use to analyze spectra. Every combination of sine waves is both a wave of one frequency with fluctuating amplitude, and two different waves. At the two limits for our potential perspectives, every sine wave is the temporally fluctuating amplitude of a constant value (evolution is everything), and every fluctuating sine wave is really a spectrum of constant, unchanging waves (repetition is everything). There is no “correct” position between the two.
Beat frequencies, then, are just as real as spectra. When we consider small enough periods of time, we hear them. But they exist whether or not we can directly perceive them, and they can become audible when we process waveforms in certain ways. Specifically, if we use some device to change the wave shape based on the amplitude (distortion, which we will cover later), that change will be occurring at a frequency equal to the beat frequency, because the amplitude is fluctuating at that frequency. The beat frequency and its harmonics will then be added to the original spectrum.
Combining Complex Waves
As we have seen, the wave shape of complex waves usually changes when we combine two waves of different phases. We can understand this by thinking of each wave as a spectrum, a collection of sine waves all added together. Each harmonic of the complex wave combines with a corresponding harmonic of the other complex wave according to what we have already said about combining sine waves. The result is the spectrum of the new complex wave.
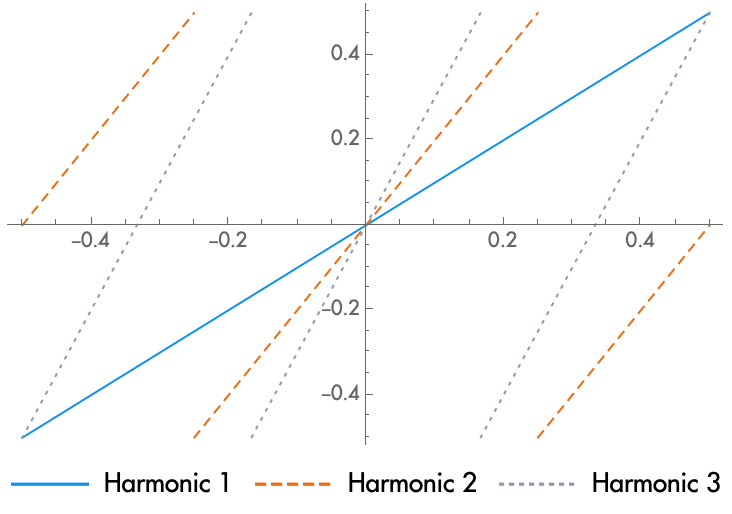
It is important to note, however, that a phase difference at the fundamental frequency of the wave will equal a different phase difference for the other harmonics of the complex wave. As you increase the phase difference between two sine waves, the waves move out of alignment, reach a negative alignment, and then approach alignment again. The amount of delay necessary to complete this cycle is equal to the period of the wave. Likewise, a delay of a fraction of a period is a phase difference of that same fraction of a cycle. A complex periodic wave can be decomposed into a series of sine waves where the frequency of each wave is an integer multiple of the fundamental frequency, \(f, 2f, 3f, ...\). A phase difference in the fundamental of some fraction of a cycle will then be twice that fraction for the second harmonic, three times that phase difference for the third, etc.
An important example is the delay of a wave by exactly half a cycle, such that the harmonic at the fundamental frequency is now negatively aligned. The harmonic at \(2f\) will then be aligned by \(2 \times 1/2 = 1\)—a whole cycle, and so it comes back into alignment. The harmonic at \(3f\) will be at \(3 \times 1/2 = 1\ 1/2 \) which is again in negative alignment. \(4f\) is at 2, positive alignment; \(5f\) at \(2\ 1/2\), negative, etc. When these waves are mixed, all the odd harmonics are canceled and all the even harmonics are enhanced, leaving a wave with harmonics at \(2f, 4f, 6f, ...\)—a complex wave that's one octave higher.
Sine waves are symmetrical, so changing their polarity is the same as changing their phase by a half cycle. But because the cycles of the harmonics are different lengths, this is not always true of complex waves. In fact, any complex wave with any even harmonic \(2f, 4f, 6f, ...\) will not be the same with a reversed polarity as with a half cycle delay. And conversely, any complex wave with only odd harmonics will be the same inverted as it is when delayed by half a cycle.
In nature, often a complex wave will have only odd harmonics because some natural process, such as reflection, will reverse the polarity of the wave and mix it with the original after a half cycle delay. In this case, each even harmonic is delayed by a complete number of cycles, but since the polarity of every harmonic is then reversed, the even cycles are negatively aligned, while the odd cycles are aligned. The result will only have odd harmonics, giving a less busy, “hollow” sound.
Phase and Delay
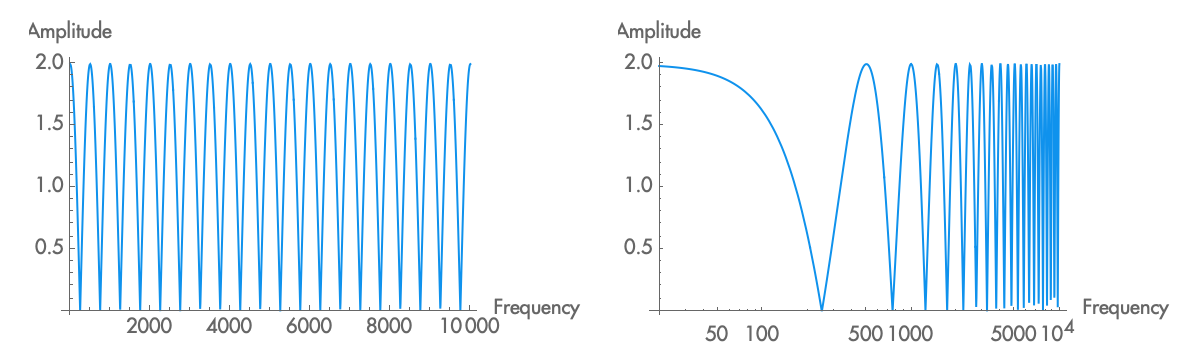
We usually talk about phase as a portion of a cycle, as a delay relative to the period of the wave. But what happens when the delay is the same no matter the frequency of the wave? Here, different frequencies are going to have different phase delays, depending on the ratio between the period and the overall delay.
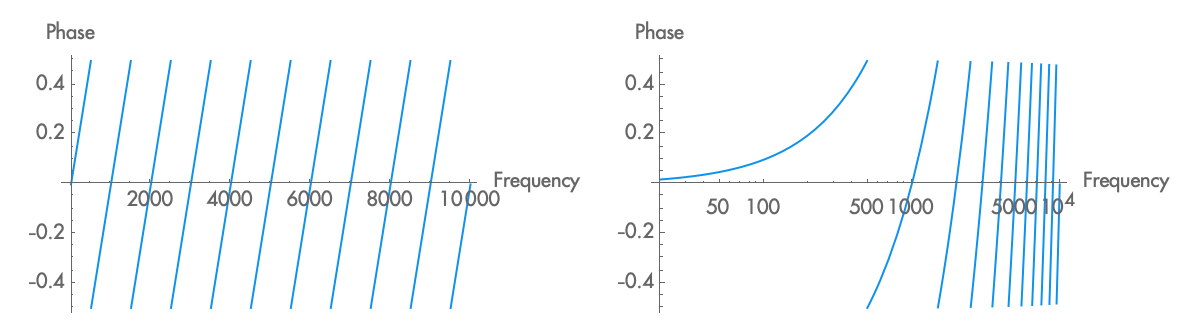
For example, if we delay by 1 ms, a wave of 1kHz will be delayed exactly 1 cycle, while a wave of 500Hz would be delayed half a cycle, and a wave of 750Hz would be delayed by three quarters of a cycle. In general, the phase delay is the ratio of the delay time to the period of the wave being delayed. We can write this as:
With a fixed delay, as you change the frequency of a wave, the wave moves out of phase, and as you change it further, it moves back into phase, then out of phase again. That is, with a constant delay, the phase is periodic with frequency. At a certain delay time, then, some frequencies will be aligned with the original signal, some will be negatively aligned, and most will be somewhere in between. When we mix the delayed wave with the original wave, then, we end up with a frequency response that is periodic with frequency. The shape of this frequency response resembles a comb, so we call this a comb filter.
The Math of Mixing Sine Waves
To write the equations for combining waves together, we need to introduce inverse functions, specifically an inverse sine wave function. A sine wave repeats, both during its cycle, and as it performs its reciprocal movement, falling after it rises, and vice versa. But if we limit the sine wave from one quarter cycle before to one quarter cycle after it crosses zero, we get a portion of a sine wave where there is a unique phase for each amplitude. The sine function gives you the amplitude for the phase, and the inverse sine function, called arcsine and denoted in equations by \(\operatorname{asin}\), gives you the phase that would produce a certain amplitude. These equations also make use of the cosine function, denoted as \(\cos\), defined above as a sine wave advanced by a quarter cycle in phase. Lastly, we use the \(\operatorname{sgn}\) function, which gives -1 or 1, depending on whether its argument is positive or negative. This mostly just carries signs out of square roots, since by convention square roots are always positive.
We can express a combination of sine waves with the following equation:
The equations for the new amplitude, \(A\), and the new phase \(\varphi\), are a little complicated, but we'll see that in practical situations they can be intuitively simplified:
When \(a\) is close to \(b\), \(a - b\) is close to zero, and the second term of the square root dominates, giving:
That is, when \(a\) is close to \(b\), the maximum amplitude of the new wave is twice the geometric average of their amplitudes (\(2 \sqrt{a b}\)), but this follows a cosine pattern from maximum alignment (relative phase is 0), to maximum disalignment (relative phase is 180 degrees). On the other hand, if one wave is much smaller relative to the other, the first term \((a - b)^2\) dominates, the overall amplitude is approximately equal to the amplitude of the bigger wave, and the smaller wave has little effect.
The phase result of combined sine waves similarly depends on the relative amplitude of the two waves. When the waves have similar amplitudes, the new phase is halfway between the first and second wave:
And conversely, when \(b\) is larger than \(a\), the arcsine term is positive and pulls the phase towards \(\phi\), the phase of \(b\), whereas when \(b\) is smaller, it pulls the new phase towards the phase of \(a\).
Lastly, these equations take on special forms when the two waves are in quadrature, with a phase difference of 90 degrees:
For waves of different frequencies, we have the following equations:
Note that to simplify the equations, the relative phase is set to zero—that is, we assume these waves start at the same time. Since the waves have different frequencies, the relative phase of the two is constantly shifting, and so it depends on when you measure it. It only makes sense to talk about the phase of this combination in general in relation to some third wave, which we won't get into here.
When the amplitudes of the two different frequencies are similar, the \(\varphi\) term disappears and we get a wave at a frequency between the two, whose amplitude is continually fluctuating at a rate proportional to the difference in frequency between the two waves. As before, an unbalanced amplitude will lessen the effect of this fluctuation and pull the effective frequency towards the wave with the higher amplitude. With similar amplitudes, we get the following simplified equations:
While ostensibly the frequency of fluctuation is half the difference between the two frequencies, this also involves a fluctuating polarity. The wave grows quieter, flips, grows louder, grows quieter, flips, grows louder again, etc. If we ignore this change in polarity, and only want to know how often it gets louder and softer, this happens at twice that frequency, or just the difference between the two frequencies.